Statistics for Queueing Theory
Queueing Theory relies on a lot of statistical theory for it's underlying
mathematics. This page contains some links to introductory statistics information
written by third parties, and an exploration of some statistical distributions
used in queueing theory. If the reader feels fully at home with the statistics
explored in this page, it can be skipped. Also, the reader may find it
easier in some cases to come back to the distributions in this page when
they are explored in more detail. Appropriate links will be provided in
these situations.
Third-Party Introductions to Basic Statistics
Note: as these are links to external sites, their quality or reliability
cannot be guaranteed. However, they were checked links as of the date this
page was last updated, and were working reliably then.
Statistical Distributions Used in Queueing Theory
While there are other distributions apart from those outlined below which
could be used for queueing theory analysis purposes, this author has not
encountered them, and these distributions seem by far to be the most popular,
and are also, according to many sources, the distributions most tractable
to mathematical analysis. More information on the distributions can be
found in the third-party pages listed above.
Degenerate (or Deterministic) Distribution
The variate in this distribution is always a constant value. This could
be used, for example, to model the input of parts to a manufacturing machine,
if one knew that the input occurred at a constant rate.
Exponential and Erlang Distributions
The exponential distribution used in queueing theory is a negative exponential
distribution. It's PDF (probability density function) is:
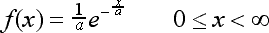
As can be seen from the equation above, the exponential distribution
has one parameter which describes it - denoted in the equation by the letter
a.
The exponential distribution is a special case of the Erlang distribution
(named after A. K. Erlang, one of the fathers of queueing theory). The
PDF of the Erlang distribution is:
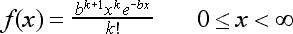
General Distribution
This does not refer to any particular statistical distribution, rather,
an arbitrary one. In other words, every other distribution is only a special
case of the general distribution, and all results derived from use of the
general distribution can be applied to any other distribution, with the
addition of the appropriate restrictions. For queueing theory purposes,
the only information one requires when applying results derived from the
General Distribution, is the mean and variance of the distribution.
Last Updated: 14th June 1999