Queues in a Bank

Introduction

As a rule people dislike queueing in banks, and so in order to improve the level of service a bank manager is interested to find out:

The average number of people waiting in the bank (i.e. the queue length)
How much of the cashiers' time is spent idle (as a percentage of their time)

Depending on how many tellers she employs during lunchtime. She is prepared to employ up to 5 cashiers, but not less than 1.

Model Assumptions and Details

The distribution of the length of time it takes the cashiers to carry out a task is exponential, with mean 2 minutes and standard deviation of 5/4 minutes
There is virtually no limit on the queue length, as the bank has a large floor area
Customers arrive in a Poisson distribution, with mean of 25 per hour
Service is done on a first come first serve basis
This is an M/M/c queue, where 1 =< c =< 5

Symbols

Symbol	Meaning, and value if in assumptions
c	Number of cashiers (servers)
Lq	Average length of the queue
W	Percentage of cashiers idle (waiting) time
	Mean arrival rate (25 per hour)
	1/(mean time to server customers) = 30 per hour
p	Average amount of work for each server, per hour

Calculations

From the above we can easily calculate the following values, which are used to work out Lq and W:
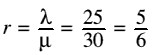
Calculating r

p0 and Lq, W and the idle time can be calculated using the following equations:
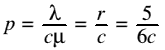
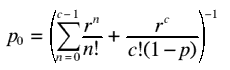
p0 derivation

The results of these equations for 1 to 5 cashiers are summarised in the following table:

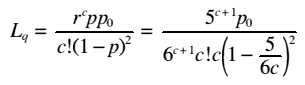
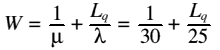
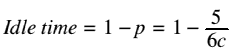
Cashiers	p	r^n / n!	p0	Lq	W	Idle
1	0.833	0.833	0.167	4.167	0.2	0.167
2	0.417	0.347	0.412	0.175	0.04	0.583
3	0.278	0.096	0.432	0.022	0.034	0.722
4	0.208	0.02	0.434	0.003	0.033	0.792
5	0.167	0.003	0.435	0.000	0.033	0.833

From the table it can be seen that either 1 or 2 cashiers should be employed, as this will keep a short queue, but without the cashiers being idle too much of the time.

Henry Morgan, 14 June 1999