Queues Forming at a Motorway Junction

Introduction

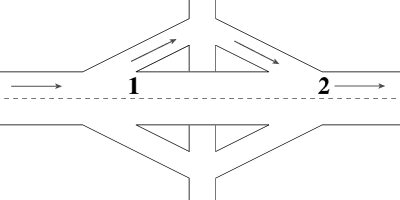
Diagram of a typical motorway junction. Point 1 is where the exit slip road meets the motorway, and point 2 is where the entry slip road meets the motorway.

This example is about how a queue caused by traffic trying the enter the motorway can then causes a secondary queue of traffic trying the leave the motorway, as the first queue backs up past the exit slip road.
Because we are interested the how the queue of traffic entering the motorway affects that trying to leave, we say that there are in fact two 'sections' to the queue formed by the merge traffic at point 2:

The traffic continuing on the motorway, past point 2
The traffic trying to leave the motorway at point 1, but can't as the exit is blocked by the continuing traffic. We shall call this the secondary queueing

Assumptions

It is the area immediately downstream of the merge point where the bottle neck occurs (as for all well laid out junctions the merge area is not the cause of the bottle neck)
The exit slip road is not a bottle neck point (ie. there is no hold up on the slip road leaving the motorway)
That the time to get between point 1 and point 2 is constant, regardless of the traffic situation. This is a needed assumption in order to avoid overly complicated expressions

Symbols

Symbol	Meaning
m	Number of lanes on the motorway
A1m(t)	Cumulative number of through vehicles that would have passed point 1 if there were no queueing
A1s(t)	Cumulative number of exiting vehicles that would have passed point 1 if there were no queueing
A2s(t)	Cumulative number of vehicles from the joining slip road that would have passed point 2 if there were no queuing
A2m(t)	Cumulative number of vehicles from the motorway that would have passed point 2 if there were no queuing
A2(t)	Cumulative number of vehicles that would have arrived at point 2 by time t if there were no queueing
D1m(t)	Cumulative number of through vehicles that have passed point one
D2(t)	Cumulative number of vehicles that have actually passed point 2
D2s(t)	Cumulative number of vehicles that have passed point 2, that came from the slip road
D2m(t)	Cumulative number of vehicles that have passed point 2, that came from the motorway
	Maximum service rate of motorway at the merge point (ie. maximum number of cars per hour that can pass point 2)
(t)	Service rate of the motorway, at point 2, at time t
s	Maximum service rate of the entry slip road
s(t)	Service rate of the entry slip road at time t
t	Time to travel from between points 1 and 2, when there is no queueing
c	Capacity of the motorway between points 1 and 2 (how many vehicles can queue in that stretch of motorway)

Modelling the traffic flow

As the traffic on the motor way can come from either the entry slip road or from the motorway we can say that A2(t) = A2s(t) + A2m(t). At first sight the number of cars (and hence the length) of the queue would appear to be A2(t) - D2(t), however this is not strictly the case, as the length of the queue is this, plus the number of cars that would have been in the area taken up by the queue, had there not been a queue. However the area between D2(t) and A2(t) on a graph of time against cumulative count gives the total delay to all vehicles that pass point 2.

Most motorway junctions are designed so that when there is a large hold up the traffic on the entry slip road will enter the motorway alternately with the traffic on the "slow lane". Thus s = /2, and so the service rate on the motorway for through traffic is -s. This also means that the through traffic on the motorway is occupying m-1/2 lanes of the motorway.

If through traffic on the motorway isn't using all of its service rate then the entry slip road's traffic can use up the slack in the system (up to the maximum limit of the slip road), and thus effectively the joining traffic gets service priority, and vice versa, when the entry slip road's traffic isn't using its full service rate then motorway through traffic can use up the slack, and so it gets service priority.
Most commonly what happens is that a queue builds up on the motorway, but the slip road remains free of queueing traffic,. as the slip road operates under its full capacity, s.
It can be said that:

D2m(t) = D2(t) - D2s(t), as the vehicles to depart from point 2 must have come from either the motorway or the slip road
D1m(t) = D2m(t) + c
A1m(t) = A2m(t + t), as if there were no queueing then the number of vehicles arriving at point 2 must be equal to the number arriving at point 1, t units of time ago, that were going to carry onto point 2

If the queue has not yet reached point 1 then A1m(t) - D2m(t) is the number of vehicles between points 1 and 2, either in a queue or moving along that stretch of motorway. Thus A1m(t) - D2m(t) - c = The number of through cars that have been delayed that have yet to reach point 1.

If we presume that there isn't a lane reserved soley for the use of exiting traffic then the exiting traffic will have to share a lane with through traffic, thus the delay for exiting traffic arriving at point 1 at a time T will be the same for a through vehicle arriving at point 1 at time T.
The delay for all through vehicles will be equal to the area between the curve of A1m(t) (which equals A2m(t + t)), and D1m(t) (which equals D2m(t) + c). Thus the delay for a single vehicle is the integral from 0 to T of (A2m(t + t) - D2m(t) - c) with respect to t / the number of vehicles:

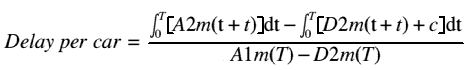
Delay caused to a car

In order for there to be no effect on traffic leaving the motorway there would need to be one lane reserved solely for traffic exiting the motorway at point 1, and in which case:

The exit junction would not affect the delay time in the queue
The queue would actually be longer, and so the speed of the queue traffic would be higher
The queue wouldn't affect the exiting of traffic

This is a solution used on many stretches of motorway, where there is enough space.

Henry Morgan, 14 June 1999