A Mail Sorting Office

Introduction

Schematic Diagram of the Sorting OfficeIn a mail sorting office the letters to be sorted often come in as a batch, and it is important to organise workers in the way that will get all the post sorted as quickly as possible.  Many post companies used to move the bulk of their workers along with the mail, i.e.  all workers were initially made to help at the start of the sorting line, to reduce the backlog, and then were gradually moved along the sorting line, as the backlog moved along it.  However Queueing Theory can be used to see if this is indeed the quickest way to sort mail, or to suggest the quickest way, if this isn't it.
For this example stage refers to a stage in the process of sorting, and server refers to a worker who sorts letters, at any stage.

Assumptions and Simplifications

 The following simplifying assumptions are made:
  1. There is a fixed number of sorters
  2. All sorters sort at a fixed, continuos rate, which is independent of which stage they are at
  3. The cumulative input to the first of the n stages is recorded
  4. The transit time of letters between stages and in stages is ignored (i.e., the time letters are in the system is due to queuing between stages)
  5. The number of letters in the system doesn't affect the system performance
  6. There are so many servers that we can ignore that fact that they are distinct servers,
The following symbols are used:
 
Symbol Represents
n Number of stages (the stages are  numbered from 1 to n)
Ak(t) Cumulative number of letters that have arrived at the stage number k
Dks(t) Cumulative number of letters that have departed from stage number k, into the input queues of the next server
Dkq(t) Cumulative number of letters that have departed the queue for stage number k
Dk(t) Cumulative number of letters that have departed from stage number k, this is equivalent to Dkq(t), as all letters that go into a server must also leave the server, and by our assumptions letters spend a negligible time in the server.
mu The service rate for all servers combined
muk The service rate for the kth stage

Positioning the Workers

By the fact that muk(t) is the service rate of the kth stage then:
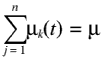
Finding muk(t)
We want to either:
  1. minimise the total delay through the system (i.e.,  each letter is in the system for the smallest possible time), or:
  2. maximise the number of letter that have departed the system after a given time
Both of these can be achieved by maximising Dn(t).  This is constrained by the values of Dk(t) for previous stages, as the final output can't be more that the output from previous stages.  Thus:

COnstrainst to Dn(t).

The acheive either a. or b. we wish to maximise Dn(t), hence:

Maximising Dn(t)

Hence all the stages should have the highest possible service rate, which is thus mu/n, this would yield the highest Dk(t) for all k.
It is never good to have a mu(k-1)> muk, as this will create a queue between stages k-1 and k, and the excess service rate used to create the queue could have been better used at the next stage to avoid the queue forming in the first place.

Summary of Results

  1. It is best to have the Postal Workers sorting mail distributed evenly between all the stages
  2. It is never advantageous to have a muk greater then the next stage.
Henry Morgan, 14 June 1999